cw2vec是蚂蚁金服2018年提出的基于笔画的中文词的embedding 方法。文中作者提到利用笔画级别的信息对于改进中文词语嵌入的学习至关重要。具体来说,首先将词转化为笔画序列,然后通过对笔画序列进行n-gram来捕获中文单词的语义和形态信息。
实现的代码地址: https://github.com/lonePatient/cw2vec-pytorch
1.介绍
我们知道,在中文中,每个单词的字符个数往往比英文单词少,每个字符包含了丰富的语义信息。但是字符级的信息足以恰当地捕捉单词的语义信息吗?是否还有其他有用的信息可以从单词和字符中提取出来,以更好地捕抓单词的语义?例如,两个单词“木材”和“森林”在语义上紧密相关。然而,“木材”由“木”和材”两个字符组成,而“森林”由“森”和“林 ”两个字符组成。如果仅考虑字符级信息,很显然该两个单词由不同的字符组成,那么在这两个单词之间是没有共享的信息。另外,如图1(a)所示,“日”作为“智”的一部分,但是几乎不包含与"智"相关的任何语义信息。除了传统的偏旁部首,再来看看另一种形式,如图1(b)所示,“智”被分解为“矢”,“口”和“日”组合。同样,直观感觉上来看这些元素与’智’的语义无关。而图1©中的“知”一定程度表达了“智”的语义信息。
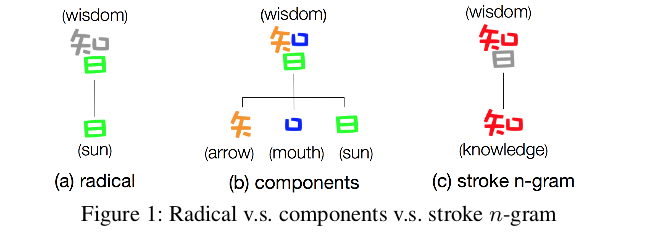
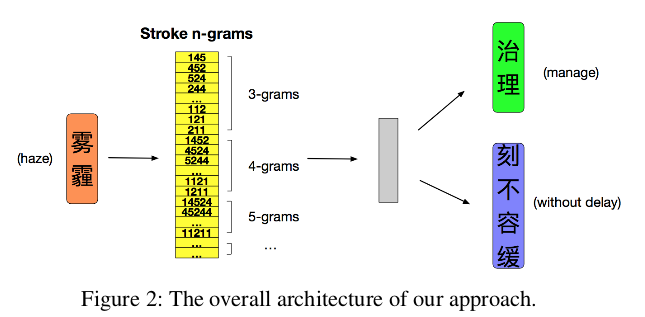
首先,将当前词表示为词的笔画n-gram,其中每个笔画n-gram都用一个向量表示,即笔画n-gram嵌入。另外,假定当前词的上下关联词的词embedding维度与笔画embedding维度相同,且不同位置的同一个词使用相同的词embedding。
2.1笔画n-gram
作者将笔画分为五种不同的类型,如图3所示:


- (1)将当前单词分割成字符组合,例如:“大人” 拆解为 “大” 和 “人”
- (2)从每个字符中分割出笔画序列并将它们连接在一起,例如:“大” 和 “人” 拆解为 “一,丿,乀,丿,乀”。
- (3)将原始笔画序列映射为ID序列,例如: “一,丿,乀,丿,乀” 映射为 13434。
- (4)通过大小为n的滑动窗口以产生笔画n-gram序列。例如:134,343,434;1343,3434,13434。
2.2 目标函数
主要通过计算单词与其上下文词之间的相似度。在大多数以单词为最小粒度的模型中,当前单词w与其上下文单词c之间的相似性被定义为:
其中,(S) 为由笔画 N-gram 构成的词典, 为词 (w) 对应的笔画 N-gram 集合,(q) 为该集合中的一个笔画 N-gram, 为 (q) 对应的向量。
我们感兴趣的是根据当前词w对上下文词c的预测进行建模。则可以使用softmax函数来模拟给定w的预测概率:
其中是词汇表V中的单词。我们知道直接计算分母可能非常耗时,因为它涉及次操作。为了解决这个问题,一般采用负采样方法。负采样的主要思想是基于数据分布,用“负”采样的上下文词汇来代替计算。则可得到目标函数为:
其中,D为语料中的全部词语, 为给定的词 w和窗口内的所有上下文词,,为负采样的个数, 表示负样本 c’按照 D 中词的分布 P进行采样,该分布可以为词的一元模型的分布 U,同时为了避免数据的稀疏性问题,类似 Word2Vec 中的做法采用 。
3.实验结果
3.1 词相似和词类比结果
备注:词类比:如已知 a 之于 b 犹如 c 之于 d。现在给出 a、b、c,看 C(a)−C(b)+C© 最接近的词是否是 d。
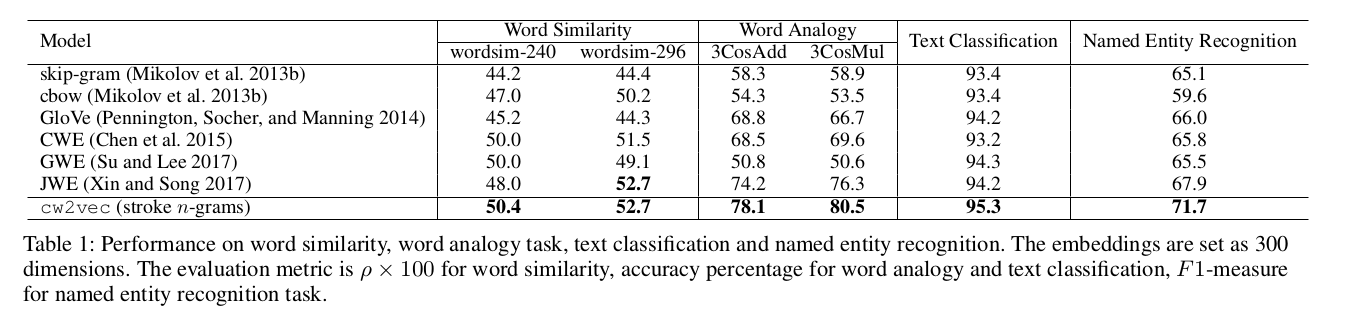
3.2 不同维度的性能对比
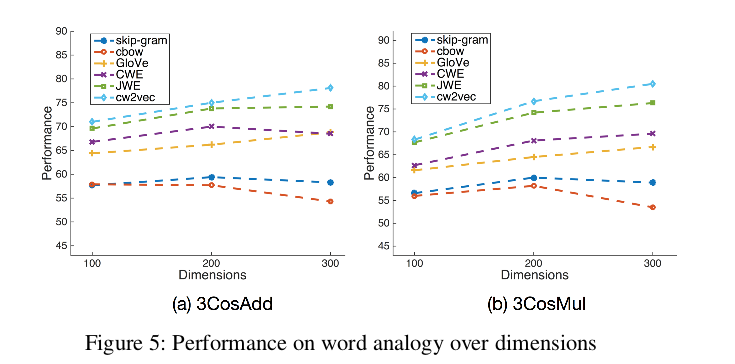
3.3 不同大小的训练数据集的性能对比
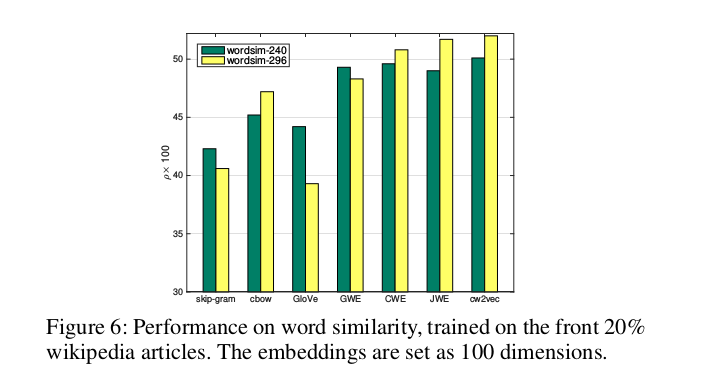
3.4 词embedding效果分析